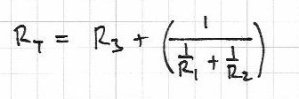Planet Arduino

Last night Massimo Banzi was Guest Judge on Intel  America’s Greatest Maker - episode 4 and had the difficult task of evaluating the teams and their projects competing in the Make or Break rounds for $100,000 and a spot in the million dollar finale.

Check some bits of the episode in this Meet and Greet video and in the Fast Forward of the episode!

 

The Following is an american TV Series which premiered last january and telling the story of

 former FBI agent Ryan Hardy (Kevin Bacon) and his attempts to recapture serial killer Joe Carroll following the latter’s escape from prison

On the 9th of April Season 1, chapter 12  aired and some of you noticed the unexpected!

An Arduino Uno spotted for the first time in a TV series at 17m 40s: Kevin Bacon jumps over an ArduinoUno-activated device … the red led blinking seems pretty dangerous!

Hello readers

Today we conclude the series of articles on the resistor. You may also enjoy part one and two.

With regards to this article, it is only concerned with direct current (DC) circuits.

Pull up and pull down resistors

When working with digital electronics circuits, you will most likely be working with CMOS integrated circuits, such as the 4541 programmable timer we reviewed in the past. These sorts of ICs may have one or more inputs, that can read a high state (like a switch being on) or a low state (or like a switch being off). In fact you would use a switch in some cases to control these inputs. Consider the following hypothetical situation with a hypothetical CMOS IC in part of a circuit from a hypothetical designer:

The IC in this example has two inputs, A and B. The IC sets D high if input A is high (5V), and low if A is low (0V). The designer has placed a button (SW1) to act as the control of input A. Also, the IC sets C high if input B is low (0V) or low if it is high (5V). So again, the designer has placed another button (SW2) to act as the control of input B, when SW2 is pressed, B will be low.

However when the designer breadboarded the circuit, the IC was behaving strangely. When they pressed a button, the correct outputs were set, but when they didn’t press the buttons, the IC didn’t behave at all. What was going on? After a cup of tea and a think, the designer realised – “Ah, for input A, high is 5V via the button, but what voltage does the IC receive when A is low? … and vice-versa for input B”. As the inputs were not connected to anything when the buttons were open, they were susceptible to all sorts of interference, with random results.

So our designer found the data sheet for the IC, and looked up the specification for low and high voltages:

“Aha … with a supply voltage of 5V, a low input cannot be greater than 1.5V, and a high input must be greater than 3.5V. I can fix that easily!”. Here was the designer’s fix:

On paper, it looked good. Input A would be perfectly low (0V) when the SW1 was not being pressed, and input B would be perfectly high (connected to 5V) when SW2 was not pressed. The designer was in a hurry, so they breadboarded the circuit and tested the resulting C and D outputs when SW1 and SW2 were pressed. Luckily, only for about 30 seconds, until their supervisor walked by and pointed out something very simple, yet very critical: when either button was pressed in, there would be a direct short from supply to ground! Crikey… that could have been a bother. The supervisor held their position for a reason, and made the following changes to our designer’s circuit:

Instead of shorting the inputs straight to supply or earth, they placed the resistors R1 and R2 into the circuit, both 10k ohm value. Why? Looking at SW1 and input A, when SW1 is open, input A is connected to ground via the 10k resistor R1. This will definitely set input A to zero volts when SW1 is open – perfect. However when SW1 is closed, input A is connected directly to 5V (great!) making it high. Some current will also flow through the resistor, which dissipates it as heat, and therefore not shorting out the circuit (even better). You can use Ohm’s law to calculate the current through the resistor:

I (current) = 5 (volts) / 10000 (ohms) = 0.0005 A, or half a milliamp.

As power dissipated (watts) = voltage x current, power equals 0.0025 watts, easily handled by a common 1/4 watt resistor. Our resistor R1 is called a pull-down resistor as it pulls the voltage at input A down to zero volts.

And with R2, when SW2 is open, input B is connected directly to 5V via R2. However. as the IC inputs are high impedance, the voltage at input B will still be 5V (perfect). When SW2 is closed, input B will be set to zero volts, via the direct connection to ground. Again, some current will flow through the resistor R2, in the same way as R1. However, in this situation, we call R2 a pull-up resistor, as it pulls the voltage at input B up to 5V.

Generally 10k ohm resistors are the norm with CMOS digital circuits like the ones above, so you should always have a good stock of them.

If you are using TTL ICs, inputs should still not be left floating, use a pull-up resistor of 10k ohm as well.

Pull-up resistors can also be used in other situations, such as maintaining voltages on data bus lines, such as the I2C bus (as used in our Arduino clock tutorials).

So that is the resistor. I hope you understood and can apply what we have discussed. If you feel something is missing, or would like further explanations, please ask.

As always, thank you for reading and I look forward to your comments and so on. Furthermore, don’t be shy in pointing out errors or places that could use improvement. Please subscribe using one of the methods at the top-right of this web page to receive updates on new posts. Or join our new Google Group.

Otherwise, have fun, be good to each other – and make something!

Thank you!

Hello readers

Today we continue with the series of articles on basic electronics with this continuation of the article about the resistor. Part one can be found here.

With regards to this article, it is only concerned with direct current (DC) circuits.

In this chapter we will examine how two or more resistors alter the flow of current in various ways. First of all, let’s recap what we learned in the previous chapter.

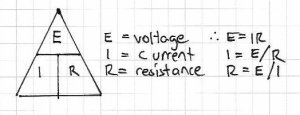
Ohm’s Law – the relationship between voltage, current and resistance:

Resistors in series:

Resistors in parallel:

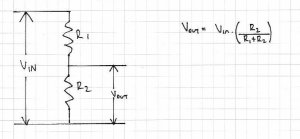
Dividing voltage with resistors:

However the fun doesn’t stop there. As there is a relationship between voltage, current and resistance, we can also divide current with resistors. For now we will see how this works with two resistors. Please consider the following:

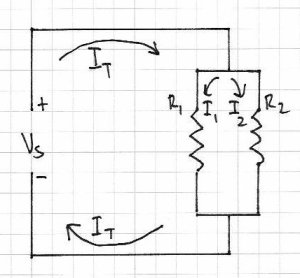
There is a balance between the two resistors with regards to the amount of current each can handle. The sum of the current through both resistors is the total current flowing through the circuit (It). The greater the resistance the less current will flow, and vice versa. That is, they are inversely proportional. And if R1 = R2, I1 = I2. Therefore, I1/I2=R2/R1 – or you can re-arrange the formula to find the other variables.

Here is an example of doing just that:

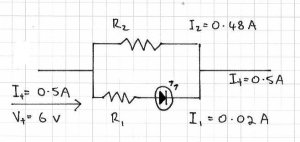
Our problem here – there is 6 volts DC at half an amp running from left to right, and we want to use an indicator LED in line with the current. However the LED only needs 2 volts at 20mA. What value should the resistors be?

First of all, let’s look at R1. It needs to change 6V to 2V, and only allow 20 mA to pass. R=E/A or R= 4 volts /0.2 amps = 200 ohms.

So R1 is 200 ohms. I1 is .02 A. Now we know that the total current is equal to I1+I2, so I2 will be 0.48A. That leaves us with the known unknown R2  We can re-arrange the formula R2/R1=I1/I2 to get R2 = (R1 x I1)/I2 – which gives us R2 of 8.3 ohms. Naturally this is a hypothetical, but I hope you now understand the relationship between the current through the resistors, and their actual resistance.

What we have just demonstrated in the problem above is an example of Kirchhoff’s current law (KCL). Gustav Kirchhoff was another amazing German physicist who worked on the understandings of electrical circuits amongst other things. More on GK here. His current law states that the amount of current entering a junction in a circuit must be equal to the sum of the currents leaving that junction. And not-coincidentally, there is also Kirchhoff’s voltage law (KVL) – the amount of voltage supplied to a circuit must equal the sum of the voltage drops in the circuit. These two laws also confirm one of the basic rules of physics – energy can not be created nor destroyed, only changed into different forms.

Here is a final way of wrapping up both KCL and KVL in one example:

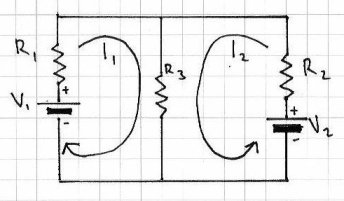
The current through R3 is equal to I1 + I2

Therefore, using Ohm’s law, V1 = R1I1 + (R3 x (I1+I2)) and V2 = R2I2 + (R3 x (I1+I2))

So with some basic algebra you can determine various unknowns. If algebra is your unknown, here is a page of links to free mathematics books, or have a poke around BetterWorldBooks.

There is also another way of finding the currents and voltages in a circuit with two or more sources of supply – the Superposition Theorem.

This involves removing all the sources of power (except for one) at a time, then using the rules of series and parallel resistors to calculate the current and voltage drops across the other components in the circuit. Then once you have all the values calculated with respect to each power source, you superimpose them (by adding them together algebraically) to find the voltages and currents when all the power sources are active. It sounds complex, but when you follow this example below, you will find it is quite simple. And a lot easier the th.. fourth time.  Just be methodical and take care with your notes and calculations. So let’s go!

Consider this circuit:

With the Superposition theorem we can determine the current flowing through the resistors, the voltage drops across them, and the direction in which the current flows. With our example circuit, the first thing to do is replace the 7V power source with a link:

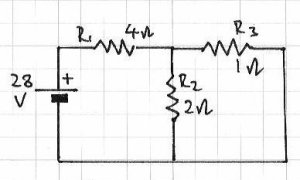
Next, we can determine the current values. We can use Ohm’s law for this. What we have is one power source, and R1 which is in series with R2/R3 (two parallel resistors). The total current in the circuit runs through R1, so calculate this first. It may help to think of the resistors in this way:

Then the formula for Rt is simple (above), and Rt is And now that we have a value for Rt, and the voltage (28V) the current is simple:

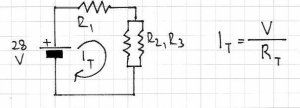
Which gives us a value of 6 amps for It. This current flows through R1, so the current for R1 is also 6 amps.

Next, the current through R2:

Using Kirchhoff’s Current Law, the current flowing through R2 and R2 will equal It. So, this is 4 amps.

At this point, note down what we know so far:

For source voltage 28V, Ir1 = 6A, Ir2 = 2A and Ir3 = 4A; R1=4 ohms, R2 = 2 ohms, R3 = 1 ohm.

Now – repeat the process by removing the 28V source and returning the 7V source, that is:

The total resistance Rt:

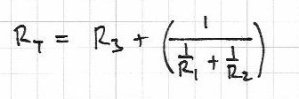
Gives us Rt = 2.3333 ohms (or 2 1/3);

Total current It will be 7 volts/Rt = 3 amps, so Ir3 = 3;

So Ir2 = 2A – therefore using KCL Ir1 = 3-2 = 1A.

So, with 7V source: Ir1 = 1A, Ir2 = 2A and Ir3 = 3A.

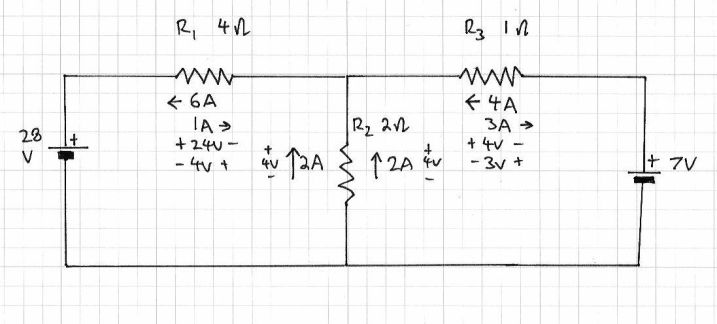
Next, we calculate the voltage drop across each resistor, again by using only one voltage source at a time. Using Ohm’s law, voltage = current x resistance.

For 28V:

Vr1 = 4 x 6 = 24V; Vr2 = 2 x 2 = 4V; Vr3 = 4 x 1 = 4V. Recall that R2 and R3 are in parallel, so the total voltage drop (24 + 4V) = 28 V which is the supply voltage.

Now, for 7V:

Vr1 = 4V, Vr2 = 4V, Vr3 = 3V.

Phew – almost there. Now time to superimpose all the data onto the schematic to map out the current flow and voltage drops when both power sources are in use:

Finally, we combine the voltage values together, and the current values together. If the arrow is on the left, it is positive; on the right – negative. So:

Current – Ir1 = 6 – 1 = 5A; Ir2 = 2 +2 = 4A; Ir3 = 4-3 = 1A;
Voltage – Vr1 = 24 – 4 = 20V; Vr2 = 4 + 4 = 8V; Vr3 = 4 – 3 = 1V.

And with a deep breath we can proudly show the results of the investigation:

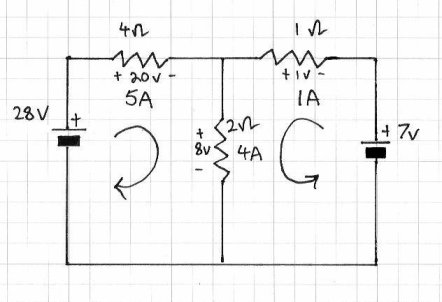
So that is how you use the Superposition theorem. However, there are some things you must take note of:

• the theorem only works for circuits that can be reduced to series and parallel combinations for each of the power sources
• only works when the equations are linear (i.e. straight line results, no powers, complex numbers, etc)
• will not work when resistance changes with temperature, current and so on
• all components must behave the same way regardless to polarity
• you cannot calculate power (watts) with this theorem, as it is non-linear.

Well that is enough for today. I hope you understood and can apply what we have discussed today. The final chapter on resistors can be found here.

As always, thank you for reading and I look forward to your comments and so on. Furthermore, don’t be shy in pointing out errors or places that could use improvement. Please subscribe using one of the methods at the top-right of this web page to receive updates on new posts. Or join our new Google Group.

Otherwise, have fun, be good to each other – and make something!

Notes: In writing this post, I used information from allaboutcircuits.com, plus information  from various books by Forrest Mims III and “Practical Electronics Handbook” 4th ed., Ian Sinclair. And used a lot of paper working out the theorem for myself. Thank you!